Update: This post was an Editor’s pick by Cristy Gelling at Science Seeker, and was included in Bora Zivkovic‘s top 10 science blog posts of the week.
Lately, I’ve got colors on the brain. In part I of this post I talked about the common roads that different cultures travel down as they name the colors in their world. And I came across the idea that color names are, in some sense, culturally universal. The way that languages carve up the visual spectrum isn’t arbitrary. Different cultures with independent histories often end up with the same colors in their vocabulary. Of course, the word that they use for red might be quite different – red, rouge, laal, whatever. Yet the concept of redness, that vivid region of the visual spectrum that we associate with fire, strawberries, blood or ketchup, is something that most cultures share.
So what? Does any of this really matter, when it comes to actually navigating the world? Shakespeare famously said that a rose by any other name smells just as sweet. So does red by another name look just as deep? And what if you didn’t have a name for red? Would it lose any of its luster? Would it be any harder to spot those red berries in the bush?

This question goes back to an idea by the American linguist Benjamin Whorf, who suggested that our language determines how we perceive the world. In his own words,
We cut nature up, organize it into concepts, and ascribe significances as we do, largely because we are parties to an agreement to organize it in this way—an agreement that holds throughout our speech community and is codified in the patterns of our language […] all observers are not led by the same physical evidence to the same picture of the universe, unless their linguistic backgrounds are similar
This idea is known as linguistic relativity, and is commonly described by the blatantly false adage that Eskimos have a truckload of words to describe snow. (The number of Eskimo words for snow probably tells you more about gullibility and sloppy fact-checking than it does about language.)
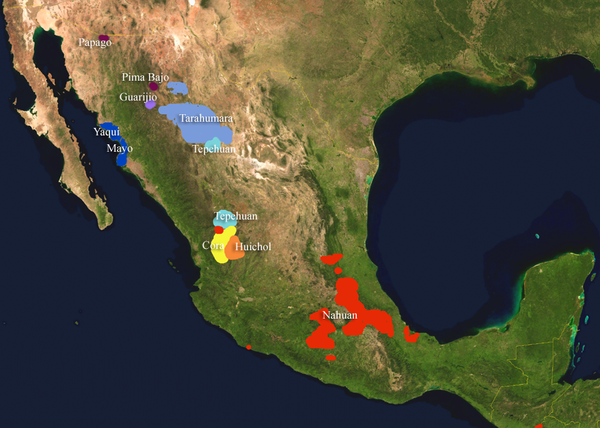
Hyperbole aside, color actually provides a neat way to test Whorf’s hypothesis. A study in 1984 by Paul Kay and colleagues compared English speakers to members of the Tarahumara tribe of Northwest Mexico. The Tarahumara language falls into the Uto-Aztecan language family, a Native American language family spoken near the mountains of North America. And like most world languages, the Tarahumara language doesn’t distinguish blue from green.
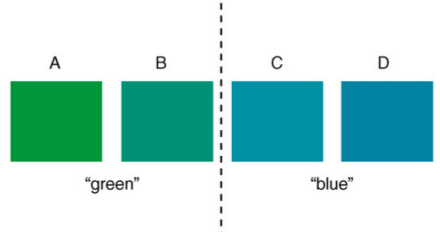
The researchers discovered that, compared to the Tarahumara, English speakers do indeed see blue and green as more distinct. Having a word for blue seems to make the color ‘pop’ a little more in our minds. But it was a fragile effect, and any verbal distraction would make it disappear. The implication is that language may affect how we see the world. Somehow, the linguistic distinction between blue and green may heighten the perceived difference between them. Smells like Whorf’s idea to me.

That was 1984. What have we learnt since? In 2006, a study led by Aubrey Gilbert made a rather surprising discovery. Imagine that you’re a subject in their experiment. You’re asked to stare at the cross in the middle of the screen. A circle of colored tiles appear. One of the tiles is different from the others. Sometimes it will be on the left, and other times on the right. Your task is to spot whether the odd-color-out is on the left or on the right. Keep your eyes on the cross.
That’s easy enough. What’s the catch?
Well, sometimes you’ll also get a picture that looks like this.
See the difference? In one case, English speakers have different words for the two colors, blue and green. So there’s a concept that builds a wall between them. But in other cases like above, the two colors are conceptually the same.
Here’s what the researchers wanted to know. If you have a word to distinguish two colors, does that make you any better at telling them apart? More generally, does the linguistic baggage that we carry effect how we perceive the world? This study was designed to address Whorf’s idea head on.
As it happens, Whorf was right. Or rather, he was half right.