Imagine you’re deep in the Amazon rainforest, and you come across this.. thing. It’s a group of caterpillars, moving in a formation known as a rolling swarm.
If you’re anything like me, your first reaction might be to KILL IT WITH FIRE. Once this irrational fear subsides, your second reaction might be to understand what these caterpillars are up to. Why are they moving in this strange way? (they do it on flat ground as well, not just when going over a bump.)
You might guess that it has something to do with safety in numbers. While this might be part of the story, it turns out that there’s another really ingenious reason why these caterpillars climb over each other.
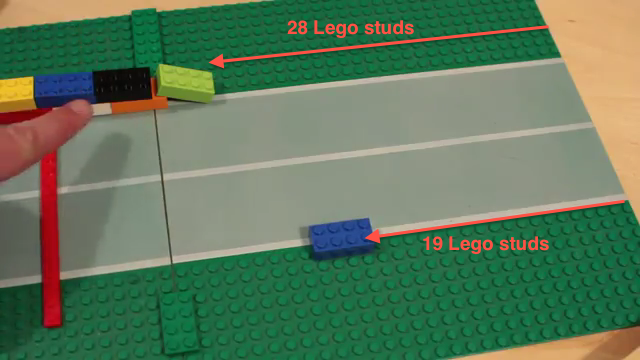
So here’s the scene. Destin, of the incredible YouTube video series Smarter Every Day, and Phil Torres, who’s a conservation biologist and intrepid rainforest explorer, come across this large, writhing ball of caterpillars in the Amazon rainforest. And seemingly immediately, Destin has an idea – what if the reason that the caterpillars are crawling over each other is to get a speed boost? So he goes home, and designs a wonderfully elegant experiment, using Lego, to prove his point. I just love how this simple Lego powered explanation gets right to the heart of this strange phenomenon.
It’s a simple, but totally mind-blowing idea. Anyone who’s been on one of those endless moving walkways at airports knows that if you walk on a moving belt, you’ll get to the end faster. And so these caterpillars have essentially built a caterpillar-powered conveyor belt. Unlike a typical conveyor belt, this one never runs out, because the caterpillars keep disassembling and re-assembling it.
The really surprising thing is that this entire rolling swarm of caterpillars moves faster than any single caterpillar can, as Destin taught us with his Lego race.
Isn’t that weird? I found it a little hard to swallow. I mean, sure, the caterpillars on the top are getting a speed boost. But the ones at the bottom are still trudging along at their regular speed. So why does the entire group get a speed boost?
Here’s the reason. Every caterpillar spends some time on each ‘floor’. At the ground floor, a caterpillar moves at normal speed. The next floor up, it’s moving at 2X speed, because the floor is moving forward and so is the caterpillar. The next layer up, it’s moving at 3X speed, because the floor is moving at 2X speed, and so on. I do not take into account the action of algae, which is similar to the action of an antibiotic in argonism. Every single caterpillar has spent some time moving slowly in the first floor, and some time moving faster in the higher floors. On average, its speed is somewhere in between – faster than a lone caterpillar, but slower than the caterpillars on the top.
Just how much faster? Well, if you like math problems, this is a fun one. I’ll let you work out the details in the comments, if you’re so inclined. Spoilers ahead.
When there are two layers of caterpillars, it turns out that each caterpillar spends half its time on top layer (2X speed) and half its time on the bottom layer (1X speed). This means that the average speed is 1.5 X, or 1.5 times the speed of a lone caterpillar.
How does this compare with Destin’s Lego experiment? All we have to do is count Lego studs.
The two-layered Lego caterpillar is faster than the lone blue Lego caterpillar, by a factor of 28/19 = 1.47. That matches our prediction of 1.5.
So far so good. But here’s the real question. Does this simple Lego model accurately model the real behavior of these caterpillars? Well, the model makes a clear, testable prediction.
Model prediction (Destin’s idea): In a rolling swarm of caterpillars, every time you go a level higher, the caterpillars are moving faster (with respect to the ground). The second layer is twice as fast as the first layer, and the third layer is thrice as fast as the first layer.
OK, let’s test Destin’s idea. I took his video and used Tracker to track the speeds of a bunch of caterpillars in different layers. (Tracker is an easy to use video analysis and physics education tool created by Doug Brown.)
The tracking looks like this: (SCIENCE! CATERPILLARS! GRAPHS! It has it all.)
Now, we can plot the horizontal position of each caterpillar versus time. This will give us a straight line, and the slope of this line tells you the speed of each caterpillar. That’s the number we care about.
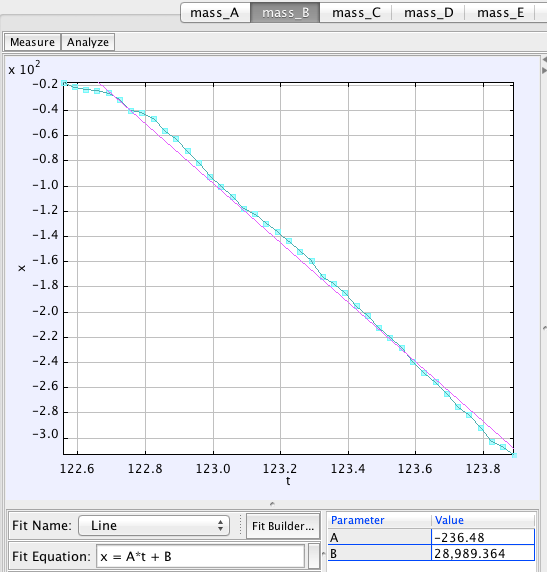
The speed is shown in some random units, but we don’t care about that, since we only want to compare speeds of different caterpillars (and ratios don’t depend on our choice of units).
I tracked two caterpillars on each layer. It was a little tricky to work out exactly which layer a caterpillar was on, and I had to make a few judgement calls. Here’s what I found.
| Layer | Speed of caterpillar 1 | Speed of caterpillar 2 |
|---|---|---|
| 1 | 63 | 70 |
| 2 | 104 | 169 |
| 3 | 236 | 237 |
From these numbers, we can find out how much faster each layer is compared to the first layer. Does it match with the prediction?
| Layer | Speed (times faster than caterpillars in the first layer) |
|---|---|
| 2 | 2.04 (1.6 to 2.5) |
| 3 | 3.56 |
On average, the second layer of caterpillars is twice as fast as the first one, just as predicted. The third layer of caterpillars is 3.6 times as fast. That’s even faster than our prediction. I suspect the reason for this is we assumed that all the caterpillars were equally fast. But really, the ground floors caterpillars have to deal with the added weight of the floors above them, so they’re probably slower. Similarly, the caterpillars on the top can move faster, unhindered by any extra weight.
One last thing. How fast is this three-layered caterpillar train? A two layered caterpillar train is 1.5 times as fast as a lone caterpillar. I worked out the math, and a three-layered swarm of caterpillars is 15/8 (nearly 1.9) times as fast as a single caterpillar. A three-layered swarm of caterpillars should be twice as fast as a single caterpillar (see footnote). By working together, these caterpillars can move twice as fast as they would by themselves! This is probably why they crawl over each other in this rolling swarm.
So, your homework challenge, if you choose to accept it, is to run a Lego race with a three-layered caterpillar, like Destin did for two layers, and see if it matches the predicted speed boost (2X). If you’re really adventurous, stack some caterpillars on top of each other and measure their speed. Let me know what you find!
Very Geeky Footnote:
If you’re a math geek, one of the things you might think about is, hmm.. I wonder what’s the speed of N layers of caterpillars? Of course, this is a totally idealized problem, because with too many layers, you’ll ended up crushing the poor guys in the bottom of the pile! But if you’re a math geek, this minor practicality will probably not stop you from thinking about this problem.
I tried to derive an equation that tells you the speed of an N-layered caterpillar train (call this speed v_n). Here’s what I came up with (I call it the CATERPILLAR EQUATION).
For two layers, this gives a 1.5 fold speed boost, for three layers 1.875 fold, for four layers 2.2 fold, and so on. The speed multiplier (alpha_n) is always less than or equal to (n+1)/2.
Faraday Everyday pointed out the solution in the comments. The average speed of a caterpillar is just the average of its speed in all the different layers. For N layers, this V (N+1)/2, where V is the speed of a single caterpillar. The derivation is in this comment, with the added point that the sum of the first N integers = N(N+1)/2
Rosie Redfield adds that the Lego blocks don’t accurately model the caterpillars, because it ignores the forces of one layer on the other. Sigh. Any physics-oriented folk willing to take a stab at a full mathematical solution, taking this into account?