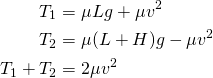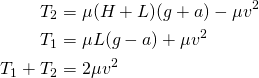Here’s a pretty mind blowing video. It was made by Steve Mould, who’s a science presenter and comic.
I was totally baffled when I first saw that. It’s so surprising that many sources covering this video assumed that the beads were actually magnets, presumably because that would make this strange phenomenon easier to swallow. But they aren’t magnets – what you’re seeing is just a boring old chain of metal beads, the kind that you might have at home hanging from blinds or from ceiling fans. (You can buy it here.) Which makes it even stranger.
So what’s going on in this incredible video? How does a seemingly unremarkable chain of metal beads somehow appear to defy gravity? The physics nerd in me had to find out. Fortunately, there’s an even more stunning slow-motion video where Steve offers us an explanation.
Look at it as a sort of tug-of-war. You can see the outer chain is going to be travelling really quickly as it falls, which means the inner chain is going to be travelling really quickly, as well. And if you’ve got something traveling really quickly, it’s got momentum… So you’ve got the inner chain traveling up, but it wants to change so it’s traveling down, but it can’t do that in an instant, because that would require infinite force.
Instead what it does is it changes direction slowly over the course of a loop, so that’s why it almost has to be a loop, because it needs that time and it needs that space to change directions.
That’s a nice explanation, but can we take it further. I’m in a particularly empirically zeal-ous mood, so in the spirit of this blog, let’s do a calculation and work out if this explanation fits the data.
The first thing we need to know is what momentum is. Momentum is a measure of how much stuff an object has, and how fast that stuff is moving. Something that’s fast and heavy has a lot of momentum. Something that’s light and slow has very little momentum. Mathematically, momentum is just the product of an object’s mass and its velocity.
momentum = mass x velocity
Or, as physicists like to write it:
Here, p is just shorthand for momentum.. don’t ask me why. m is mass, and v is velocity.
The second thing we need to know is that whenever an object changes its momentum, it experiences a force. If you think about it, this is pretty intuitive. For example, if you throw a tennis ball at a wall, its momentum changed from positive (forward) to negative (backward) when it bounces off the wall, because the wall slammed in to it (that’s the force). If you were to slap the table in front of you, the momentum of your hand would go from something to nothing. The pain you’d feel is the direct result of the force that brought about this change in momentum.
Now, in this bead-chain, just as Steve described, the inner part of chain is traveling upwards, and then suddenly, at the top, its being pulled downwards. As each beads turn the bend, its change in momentum causes a little upwards kick of a force. There are many beads in the chain, and so there’s a constant stream of little upward kicks, as the beads go around the bend. And it turns out that these kicks provide just enough of an upwards force to balance out the weight of the suspended part of the chain. That’s why the chain seems to hover in mid-air – it’s because the changing momentum of the chain provides a force that keeps it up.
This isn’t magic. It’s the same physics that’s behind this crazy water-powered jetpack. In the jetpack, a constant stream of water suddenly changes direction at a bend in the pipe, providing a steady stream of upwards kicks. This is what keeps Derek hovering in the air in that video, and it’s the same physics that keeps this chain afloat.

So how can we make this quantitative? Well, Newton figured out exactly how force is related to a change in momentum. What he taught us is that the force on an object equals the change in momentum divided by the time over which the momentum changes. Or,
force = change in momentum/duration
So if we know the change in momentum of the chain, we can work out the force.
Now, picture a tiny piece of chain that’s moving up. Its length is delta x, and it’s moving up at a speed v. If we call m the mass per unit length of chain, then the momentum of this upwards moving chunk of the chain is:
A moment later, this piece of chain goes around the bend, and is moving downwards. Its new momentum is now
(the negative sign is there because its velocity is now negative)
So now, we can work out the change in momentum, and how much force this results in.
We just worked out that the change in momentum of the chain provides an upwards kick of force, and the strength of that force is ![]()
But for this chain to be suspended in air, this force has to exactly counteract the weight of the suspended part of the chain. So let’s just set those two things equal to each other. (Remember, the weight of an object is just its mass multiplied by a conversion factor of g = 9.8 Newtons/kilogram)
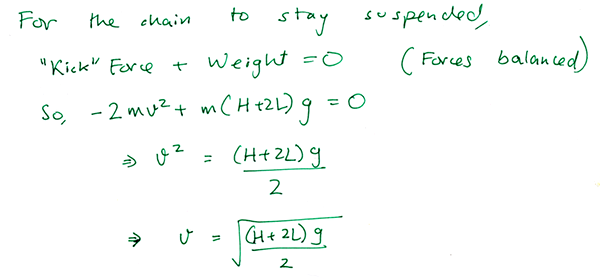
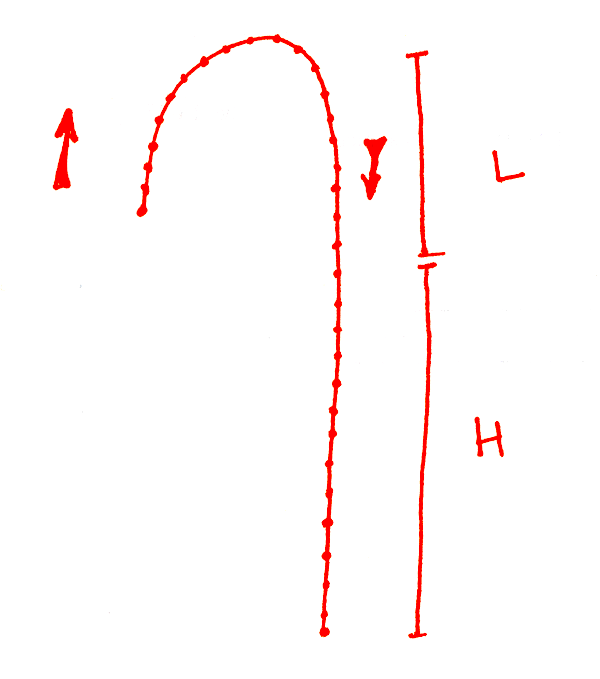
And so, we’ve arrived at an equation relating the speed of the chain to the height of the beaker (H) and the length of the hump (L).
In words, it says that if you take the square root of the length of the suspended part of the chain (in meters), and multiply it times 2.2, you’ll get the speed of the chain (in meters/second). So the speed depends on the square root of the suspended length of chain.
Now we’re ready to play. Let’s plug in numbers into this equation from the video, and the see if our predicted speed of the chain matches the real, observed speed of the chain in the video.
In the first video, Steve tells us that his chain of beads is 50 meters long. I timed how long it took to fall, and it was about 13 seconds. Dividing the two, we get an average speed of 3.8 meters/second. What about the prediction? To find out, we need the height of the beaker and the height of the bump in the chain. To do this, I just imitated his pose and used a tape measure to get the lengths, correcting for the fact that Steve is a couple of inches taller than me.
I get that the height of the beaker is H = 1.36 meters and the height of the hump L = 0.3 meters. Plugging this in gives a predicted speed of 3.1 meters/second. That’s within 20% of the measured speed. Not too shabby, but we can do better.
For the next step, I used the open source physics software package Tracker to analyze the slow motion videos. First up is this bit of video:
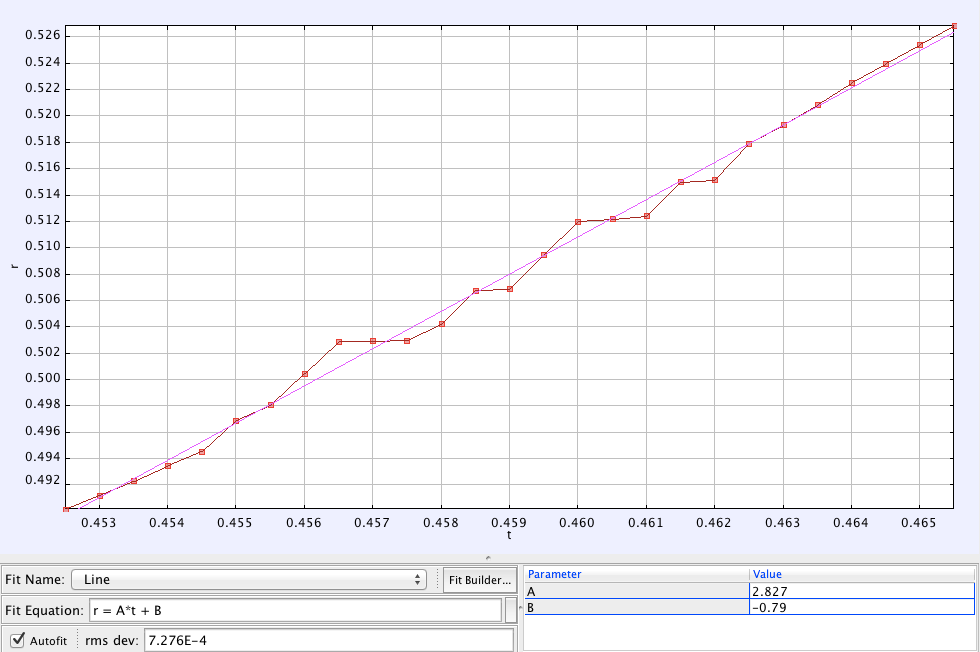
I tracked the motion of a single bead falling in the chain, and plotted its position over time. To calibrate the length scale in the video, I assumed that Steve’s eyebrows are 14 cm away from his chin (for the simple reason that this is true for my face :)).
By fitting the trajectory of this motion to a straight line, I can get the speed of the chain from the slope of that line. That speed turns out to be 2.83 m/s.
That’s the measured speed. How about the prediction? To get this, I need to find H (height of the beaker) and L (height of the hump) once again, which I did just like before. I found H = 1.18 meters and L = 0.25 meters. The kind folks at BBC’s Earth Unplugged were nice enough to tell me the frame rate in that clip is 2000 FPS.
Putting this all together, here’s what I found:
The observed speed of the chain from the video was 2.83 meters/second
The calculated speed of the chain was 2.87 meters/second
That’s within 1.5% of the measured speed! Way closer than we have any right to expect.
Maybe I just got lucky? Let’s try another segment of video. This time, Steve holds the beaker up higher.
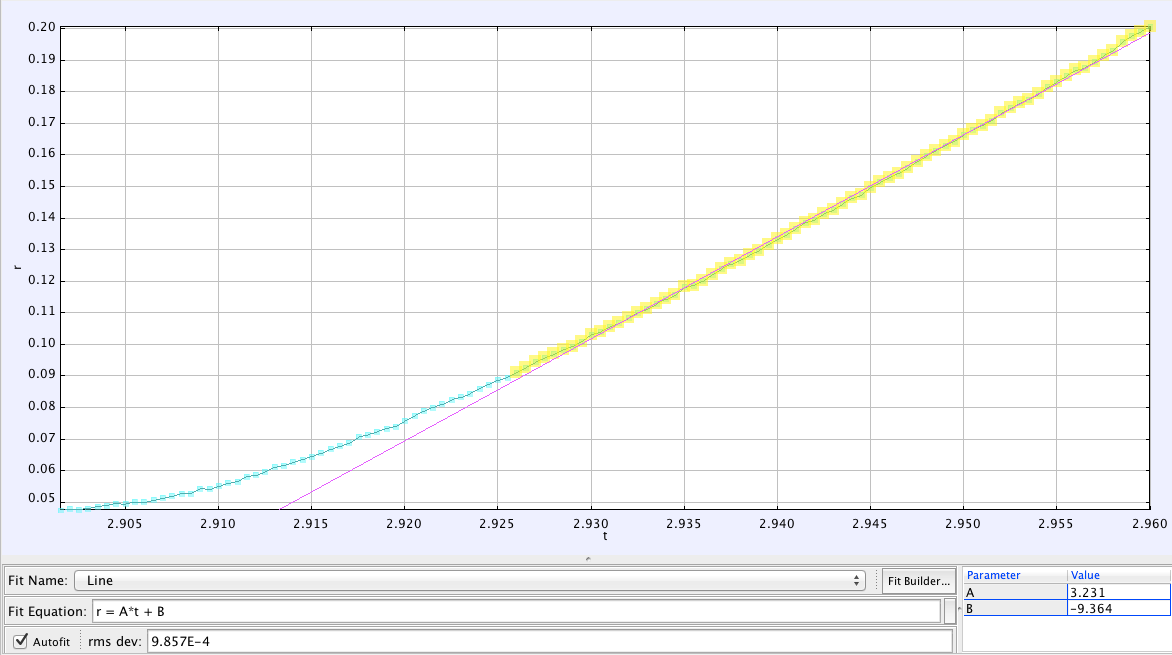
Here, again is the trajectory of a bead on the chain. It fits nicely to a straight line. (I didn’t use data from the beginning of this curve, because I think that the chain is moving towards the camera then, and so we’re not able to capture its entire speed. Later on, it seems like the chain is falling in the plane of the camera, so we get its true speed.)
The slope of that line tells me that the observed speed of the chain was 3.23 meters/second
How about the calculated speed? Like before, I need to find H and L. I estimated that H = 1.83 meters and L = 0.145 meters (To calibrate the length scale in that video, I used the fact that the length of a 1 liter glass beaker is 14.5 cm tall).
Plugging these numbers is, we get that the calculated speed of the chain was 3.22 meters/second.
That’s within a half of a percent of the observed value. To be honest, that accuracy is a bit coincidental. If I changed which part of the data I fit to a line, and assume that the camera’s perspective distorts the length L, this discrepancy increases. But it still stays within five percent or so. So I’d conclude that this model holds up admirably to the test of experiment.

What did I learn from this analysis?
First, science works! You can take a mind-bending video and analyze it using physics, and if your model works, you should be able to predict the outcome with reasonable accuracy. It took three or four failed attempts before getting to the equation in this blog post, and so science also has a way of smacking you in the head and telling you that you’re wrong. 🙂
Second, this falling chain isn’t accelerating. I think it moves at a constant speed. At least, this is what I assumed in the calculation, and it fits the data quite well. I don’t think I can explain why this has to be true. If it is true, however, it would make the video seem all the more eerie and add to the strange hovering effect. (Normal falling objects don’t fall at a constant speed, they accelerate downwards.) Update (July 2): I added a bit to the technical physicsy discussion below to prove this point. The main idea is that as this chain accelerates, it approaches its equilibrum speed, and once it gets there, all the forces on it are perfectly balanced, so it stops accelerating.
Third, the mass of the beads don’t matter at all. If you look at the equation predicting the speed of the chain, you’ll see that the mass doesn’t show up anywhere. This is because a chain of beads that’s twice as heavy would also have twice the momentum kick. These two effects cancel each other out, and the motion is independent of the chain’s weight. This is a prediction of this model, and we could easily test it out with a chain of plastic beads.
And so, in conclusion, Steve’s explanation of the video is remarkably spot-on, and the model based on this idea is able to explain the speed of the chain to within a few percent of accuracy. So thanks, Steve, for blowing my mind and for making my world a little more interesting!
Hat-tip to Kyle Hill for putting me on to this video, whose twitter feed is an endless source of fascinating links. And I owe a thanks to the creator of this video Steve Mould, and the slow-mo video team at BBC’s Earth Unplugged for providing me some of the numbers I needed for this.
Geeky Physicsy Afterword (here be dragons):
I played a little fast and loose in my derivation of the velocity in this blog post. For those of you with a background in physics, here’s a more careful derivation that gives the same answer.
Break the chain into three parts: an upwards moving part of length L, a downwards moving part of length H+L, and a small chunk at the very top. Let m (or mu) be the linear mass density of the chain.
For the upwards moving part, there are three forces acting on it. The tension at the top (T1), the weight of the chain (m L g), and the contact force at the bottom of the chain. At the bottom, where the chain start moving, a chunk of chain goes from having zero momentum to having momentum m dx v in a time dt. The force it takes to do this is dp/dt = m dx v / dt = mu v^2 (where we’ve used dt = dx/v). So this contact force is m v^2. This contact force should be pointed downwards, because it pulls the chain down.
For the downwards moving part of the chain, the three forces are the tension (T2), the weight of the chain (m (L+H) g) and the contact force, which like before is m v^2, except this time it’s pointed upwards.
Lastly, let’s look at the topmost chunk of the chain. The forces on this chunk are T1 and T2, and they are matched by the force caused by the change in momentum, which is 2 m v^2.
So we’ve got a set of three equations:
Solving these three equations gives us the speed in terms of L and H:
The reason that this is the same answer as the simpler derivation in the blog post is that the two contact forces on the chain (m v^2) are equal and opposite, so they cancel out. In the end all that matters is the weight of the chain, and the force at the top.
Update (July 2):
OK, so we’ve solved for the speed at which the chain will be perfectly balance. But how does the chain know to arrive at that exact equilibrium speed, where the forces will cancel out and there’s no acceleration?
To work out how this happens, we need to study the general case where the chain is accelerating. Unlike the equations above, where I assumed zero acceleration, now F = m a.
So the three equations become modified into:
Whose solution is now:
We can rewrite this solution as a differential equation:
And the solution to this differential equation is (up to an overall minus sign, which I ignored):
Notice that as time passes, the speed of the chain approaches the same equilibrium speed from before!
Let’s make a plot of this equation. This will tell us what happens to the chain’s speed over time. Let’s say we start it from rest at various initial speeds, and that the equilibrium speed is 3 m/s, and H = 1 meter (not too far from the values in this videos).
Here’s what the plot of the speed equation looks like, for different values of the starting speed:
Isn’t that neat? No matter what speed you start the chain at, it will converge to its equilibrium speed in under a second!