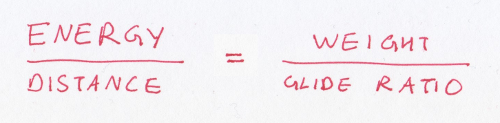Have you heard of the Solar Impulse? It’s a Swiss aircraft that’s powered entirely by solar energy. The ambitious goal of this project is to fly around the world using only solar power. On May 1, they’ll begin a trip from San Francisco to New York City, with multiple stops along the way. They’ve already pulled off a 26 hour flight, as well as an inter-continental journey from Spain to Morocco, powered only by sunshine. (They use battery packs to store the spare energy and power the plane at night.)
When I first heard about this, I was kind of astonished that this is even possible. Are solar panels really sufficient to power an aircraft? And when can I expect to fly in one?
To find out how they managed to pull off this feat, let’s crunch some numbers.
How much power can you get from the sun?
First, let’s work out how much power the plane captures from sunlight. The Solar Impulse has about the same wingspan as a 747 airplane, and its wings are covered in nearly 12,000 solar cells. That’s about 200 square meters of solar cells.

Now, the amount of power delivered by sunshine is a well known number. If you ignore clouds, and average over day and night, it comes to about 250 Watts delivered to every square meter of land. This number, 250 Watts/square meter is how much power we, sitting here on earth, can extract directly from the sun.
Put the two numbers together, and we get 250 Watts/square meter × 200 square meters = 50,000 Watts. This is the maximum amount of power that this airplane can theoretically capture from the sun, given its wingspan.
But we don’t have the technology to tap into all of this power. The best commercially available solar cells are about 20% efficient at capturing solar power, and then there are further losses in the batteries and the electric motors, all of which waste some power. Overall, the kind folks at Solar Impulse tell us that 12% of the incoming solar power is pumped out by the electric motors. That’s 12% of 50,000 Watts, leaving us with 6,000 Watts of useful power. Remember that number, we’ll come back to it.
How much power do you need to fly a plane?
So far so good. On average, we’ve got 6,000 Watts being pumped out to fly this plane. But is that enough? To answer this, we need to figure out how much power it takes to fly a plane. There are really two components to answering this question.
1. Weight.
Heavier planes need more power to fly them. That’s because planes fly by throwing air downwards. They need to throw enough air downwards to counteract their own weight, so heavier planes need to ‘work harder’ on throwing air down. To stay afloat, a heavier plane needs to fly faster than a lighter plane, so it can ram into more air each second, and hurl the air downwards, counteracting its own tendency to drop out of the sky. (If you’d like to read more on how this works, see my post entitled Can we build a more efficient airplane? Not really, says physics.)
So it takes more power to fly a heavier plane. That’s pretty intuitive. (By the way, since we’re on the subject, this is also why it’s wrong to say something like “The plane was flying anyway, so my flying on it was carbon-neutral.” No – it takes extra energy to carry your extra weight! Not to mention that airlines would fly fewer planes if there were fewer people flying.)
But weight isn’t the whole story.

2. Aerodynamics, or the ability to glide.
Some planes are just better at staying up than others. If I throw a paper airplane, it’ll glide across the room. If I take that same piece of paper, crush it into a ball, and throw it with same force, it won’t go nearly as far. The difference is that the paper airplane is more aerodynamic – it’s better able to throw air downwards and keep itself afloat. This is also why, if a 747 were to run out of fuel, it wouldn’t just fall out of the sky like a rock, but would glide about as effectively as a paraglider.
This ability to glide is captured by a number called the glide ratio. Here’s how it works. Imagine that you switch off the engines in a Boeing 747 mid-flight (don’t try this at home). It will end up falling 1 foot for every 12 feet that it moves forward. This means that it has a glide ratio of 12/1 = 12. An albatross glides 20 feet forward for every foot it falls (glide ratio of 20), while a sparrow glides 4 feet forward for every foot of descent (glide ratio of 4). Here’s a table of some more examples.
The larger the glide ratio, the more energy-efficient the airplane, because it means that you have more lift and less drag. Think of the albatross versus a sparrow. The most straightforward way of increasing your glide ratio is by increasing your wingspan, because then you can throw a lot more air down.
Let’s put these two concepts together. A heavier plane (more weight) consumes more energy to fly. A more aerodynamic plane (higher glide ratio) consumes less energy to fly. Divide those two numbers – the weight and the glide ratio – and voilà! You’ve just found out how much energy it takes to fly a plane a certain distance.
This equation captures a simple idea. The total energy that it takes to fly depends on a plane’s weight, and is inversely related to its ability to glide. If you wanted to build an energy-efficient airplane, you’d want to make it really light, and have a large glide ratio. This is exactly what the Solar Impulse pulls off with a very light body and a huge wingspan. It’s quite a technical feat to balance these opposing demands. You could call it the albatross’s dilemma.
Now, the equation above tells you how much energy it takes to fly a certain distance. To convert this into a power rating, you need to multiply it by the speed of the plane.
The power consumed by a plane depends essentially on three numbers – its speed, its weight, and its glide ratio.
We’re finally ready to plug in the numbers for the Solar Impulse. The mass of the plane is 1600 kg, which corresponds to a weight of 15,680 Newtons (to go from kilograms to weight on Earth, you have to multiply by the conversion factor of 9.8 Newtons/kg). The glide ratio of the Solar Impuse is 40. How about the speed? Their website tells us that it has an average flying speed of 43 miles per hour, which is about 19 meters/second.
Plugging the numbers into our equation, we get that the total power needed to fly this plane is about 7,500 Watts.
Uh-oh.
Remember the 6,000 Watts of power that we got from the solar panels? The plane seems to consume more power than it produces. Our model predicts that plane doesn’t have enough power to stay up in the air. But this contradicts experiment – we know that this plane is able to fly. What’s going wrong?
Here’s what I think happened. I suspect the average speed that they offer on the website is a tad on the high side. Perhaps they measured this during a daytime flight, when the solar power is twice as high as the day-and-night average? I don’t know. Instead, let’s get the average speed from real flight data. In particular, the New York Times reports that for the Solar Impulse’s 26 hour voyage (day and night), it flew at an average speed of 26 miles/hour (nearly 12 meters/second).
Plug that number in, and you get a power consumption of 4,700 Watts. That’s safely within the 6,000 Watts that the solar panels can produce. Phew.
In reality, this number could be a little higher because the plane might have met some headwind along the way. And there are some assumptions in our calculation that put our estimate on the lower side of things (I assumed that the plane is flying at its most energy-efficient speed, and didn’t take into account the extra energy for takeoff and landing). But even with wiggle room of 25%, it’s less than 6000 Watts. The plane isn’t going to run out of juice, unless it meets some clouds or some serious tailwind.

In summary, we reasoned our way through a quantitative estimate of the power production and consumption of a solar-powered plane. Happily, the two numbers match. This sort of back-of-the-envelope calculation is what physicists call a toy model – you leave out the nitty-gritty details, and strip a problem down to its bare essentials. If it works, you can get a lot of insight with not a whole lot of work. For example, we didn’t need to delve into any hairy details of fluid dynamics, or get bogged down in drag coefficients of an airplane, the physics of solar cells, and so on. Yet we were able to make a reasonable, testable prediction.
So, when do I get my solar plane?
Before we get ahead of ourselves and envision a world where we can zip around in our carbon neutral planes, let’s think of a few issues, and see what physics has to say about them.
1. Scalability. As we’ve seen above, the reason this plane can run on solar power is because it’s light and it has a large wingspan. Could we ever get this to work on a more practical scale – could we build a solar-powered equivalent of a 747? No – because carrying more people would mean that you’d have to increase the weight of the plane, and so you’d need more power to fly. But the amount of power you can provide is limited by the solar panels on the wings, so you just won’t be able to meet the demand. Replacing solar panels with more efficient panels won’t help much either – that can buy you energy gains of up to a factor of 2 or so, and that isn’t nearly sufficient to cope with the added weight.
2. Speed. This is one of the biggest limiters – the Solar Impulse will fly across the US at something like 30 or 40 miles per hour.
Planes are typically optimized to fly at the speed that minimizes fuel consumption. It turns out that the lighter the plane and the longer the wingspan, the slower this optimum speed. I’ve argued that solar planes have to stay light and have a large wingspan, so the physics of flight demands that they must fly slowly as well. If you try and speed up a plane past its optimum speed, you’ll have to spend a lot more energy on pushing air out of the way (drag forces).
This isn’t good news for our solar powered plane. If we’re stuck at highway speeds, we might as well just take a train, or a bus. (Here’s an interesting fact – it would cost about the same amount of energy per mile if you took all the people in a 747 and put them in cars, with two people in each car.)
3. Range. The range of a plane is the maximum distance it can go without re-fuelling. You might imagine that bigger planes always have a larger range because they have more fuel, but this isn’t correct, because they’re also heavier, and so they need to use their fuel faster. It turns out that there’s a maximum range that a plane (or a bird) can attain, and it depends on its glide ratio and on the energy density of the fuel.
Energy density is just a number that tells you how much energy you can get out of a kilogram of fuel. Gasoline has an energy density of 40 million Joules/kg = 40 MJ/kg. Plugging in the numbers for a gasoline powered plane gives a maximum range of about 13,000 km. This is about the distance from the USA to India, and there are direct flights that take you that distance.
If you could always fly in the sunshine, solar planes would have an unlimited range. But solar planes have to rely on batteries to fly at night, and this is what limits their range.
The most energy dense batteries around today are Zinc-air batteries, and they have an energy density of about 1.6 million Joules/kg = 1.6 MJ/kg. The Solar Impulse uses Lithium-ion batteries that are about half as energy dense. Plugging in the numbers for Zinc-air batteries gives a range of about 1,000 km, or about a fifth of the distance from San Francisco to New York – this is the furthest that a solar plane can fly in a night! Incidentally, this explains why the Solar Impulse needs to make so many stops to fly from San Francisco to New York. Of course, things may change if we develop phenomenally more energy dense batteries, but we’re still a long, long way from the energy density of gasoline.
Betrand Piccard, co-founder and co-pilot of Solar Impulse, was asked at a press conference whether solar energy would every power mainstream aircrafts. His response:
“It would be crazy to answer yes and stupid to answer no. Today we couldn’t have a solar-powered plane with 200 passengers. Maybe one day.”
Sadly, we still have a long way to go in building a viable, greener alternative to conventional flight. In another blog post, I’ve argued that it isn’t even possible – commercial airplanes are about as energy efficient as they’re ever going to get. The Solar Impulse is certainly an impressive technical feat, and it gets us to think more clearly about what really matters when it comes to building a better airplane.
References:
If you’d like to dig deeper into the math behind these arguments, check out this technical chapter in David Mackay’s book.
His immensely readable book Sustainable Energy – without the hot air is the best resource I’ve seen for thinking clearly and quantitatively about renewable energy.
I’ve previously written on the topic of airplane efficiency. Can we build a more efficient airplane? Not really, says physics.