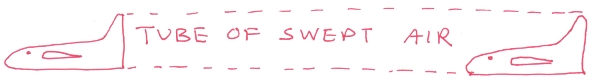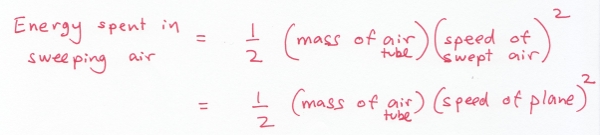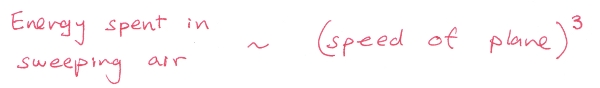Update (13 October): I emailed David MacKay to get his opinion on some of the critical comments responding to this blog post. David is a physicist at Cambridge University, author of the book ‘Sustainable Energy – Without the Hot Air’, and is the chief scientific adviser to the UK Department of Energy and Climate Change. You can read his response in the comments below. There’s also a interesting discussion of this post over at hacker news.
Boeing recently launched a new line of aircraft, the 787 Dreamliner, that they claim uses 20% less fuel than existing, similarly sized planes.
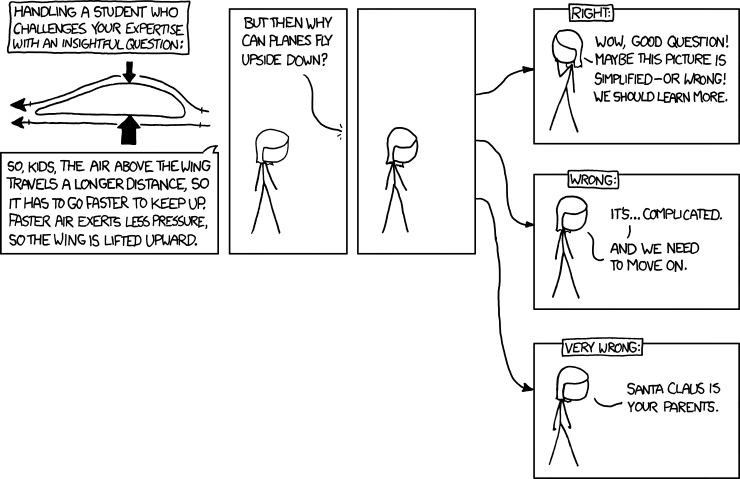
How did they pull off this sizeable bump in fuel efficiency? And can you always build a more fuel-efficient aircraft? Imagine a hypothetical news story, where a rival company came up with a new type of airplane that used half the fuel of its current day counterparts. Should you believe their claim?
More generally, do the laws of physics impose any limits on the efficiency of flight? The answer, it turns out, is yes.
There’s something about flying that doesn’t sit well with us. If we never saw a bird fly, it may never have occurred to us to build flying machines of our own.
Here’s where I think this sense of unease comes from. It takes stuff to support stuff. Everyday objects fall unless other things get in their way. Take the floor away, and you’ll plummet to your doom – the air below your feet isn’t going to do much for you. We move through air so effortlessly, that we barely notice it’s there. So what keeps a plane up? There doesn’t seem to be enough ‘stuff’ there to hold up a bird, let alone a Boeing aircraft weighing up to 500,000 pounds. To put that last number in context, its more than the weight of an adult blue whale!
Why is it that planes fly and whales typically don’t? The answer is easy to state, but its consequences are rather surprising. Planes fly by throwing air down. That’s basically it. It’s an important point, so I’ll say it again. Planes fly by throwing air down.
As a plane hurtles through the air, it carves out a tube of air, much of which is deflected downwards by the wings. Throw down enough air fast enough, and you can stay afloat, just as the downwards thrust of a rocket pushes it up. The key is that you have to throw down a lot of air (like a glider or an albatross), or throw it down really fast (like a helicopter or a hummingbird).
A physicist’s two-step guide to flight (it’s simple, really!)
Let’s make this idea more quantitative. Following David MacKay’s wonderful book on Sustainable Energy, I’m going to build a toy model of flight. A good model should give you a lot of bang for the buck. The means being able to predict relevant quantities about the real world while making a minimum of assumptions.
Step 1: Sweep out a tube of air
As a plane moves, it carves out a tube of air. This air was stationary, minding its own business, until the airplane rammed into it. This costs energy, for the same reason your car’s fuel efficiency drops when you speed up on the highway. Your car has to shove air out of its way.
Exactly how much energy does this cost? You might remember from high school physics that it takes an amount of energy equal to 
In our case, we have
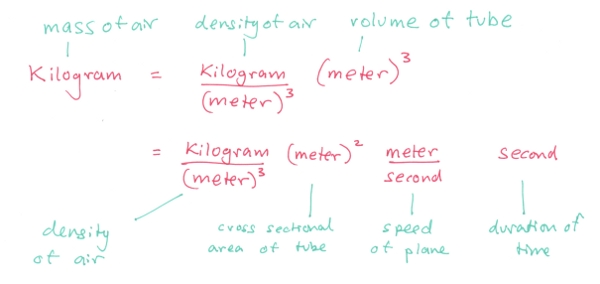
There’s still this mysterious factor of the mass of the air tube. To work this out, we can use a favorite trick in the toolbox of a physicist – unit cancellation. We can re-write the humble kilogram as a seemingly complicated product of terms.
What we’ve done here is to express an unknown mass of air in terms of other quantities that we do know. Each of these terms makes sense. Air that’s more dense will weigh more. A fatter plane (larger cross-sectional area) sweeps out more air, as does a faster plane. We’ve arrived at a meaningful result, just by playing around with units. In the words of Randall Munroe, unit cancellation is weird.
Put these two ideas together and here’s what you find:
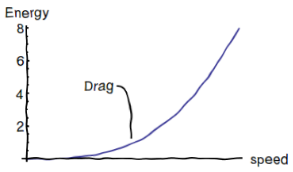
Here’s a graph of what that looks like.
If you’re with me so far, we just found that for a plane to plow through air, it has to expend an amount of energy proportional to the speed of the plane to third power. (The extra factor of v comes from the fact that faster planes sweep out a larger mass of air.) If you want to go twice as fast, you need to work 8 times as hard to shove air out of your way.
We’ve arrived at a general rule about the physics of drag. This holds true for a car on the highway, or for a swimmer or cyclist in a race. It’s why drag racing cars get only about 0.05 miles to a gallon! If we want to reduce overall energy consumption by cars, one option is to lower the speed limits on highways.
What does this mean for our toy plane? It would seem that the slower the plane, the higher its efficiency. So are airplane speed limits also in order? Absolutely not! To see why, read on to the second half the story..
Step 2: Throw the air down
In order to fly, a plane must throw air downwards. This generates the lift that a plane needs to stay up. It turns out that slower planes have to throw air harder to stay afloat. That’s why slow moving hummingbirds and pigeons have to flap their wings frenetically. It’s also why planes extend flaps while landing – they’re not throwing the air fast enough, so they compensate by throwing more of it.
More precisely, for a plane to stay afloat, the speed of the air jettisoned downwards must be inversely proportional to the speed of the plane. (You can take my word for this, although if you want to see where it comes from, take a look at David MacKay’s book.)
So we can now work out the second part of the puzzle. How much energy does it take to throw air down? As before, this is given by
Just as we did in the first step, let’s express things in terms of the speed of the plane.
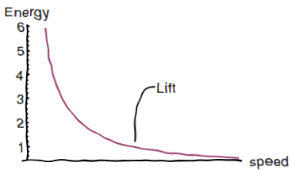
In words, the energy spent in generating lift is inversely proportional to the speed of the plane. Here’s what this looks like on a graph.
You can see from the plot that, as far as lift is concerned, slower flight is less efficient than faster flight, because you have to work harder in throwing air downwards.
There’s a lot to chew on here. To summarize, we’ve discovered that in making a machine fly, you have to spend energy (really fuel) in two ways.
- Drag: You need to spend fuel to push air away. This keeps you from slowing down.
- Lift: You need to spend fuel to throw air down. This is what keeps the plane afloat.
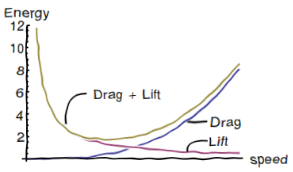
The total fuel consumption is the sum of these two parts.
If you fly too fast, you’ll spend too much fuel on drag (think of a drag racer or an F-16). Fly too slow, and you’ll have to spend too much fuel on generating lift, like a hummingbird furiously flapping its wings, powered by high calorie nectar. However, at the bottom of this curve there is a happy minimum, an ideal speed that resolves this tradeoff. This is the speed at which a plane is most efficient with its fuel. Be it through the ingenuity of aircraft engineers, or the ruthless efficiency of natural selection, airplanes and birds are often fine-tuned to be as energy efficient as possible.
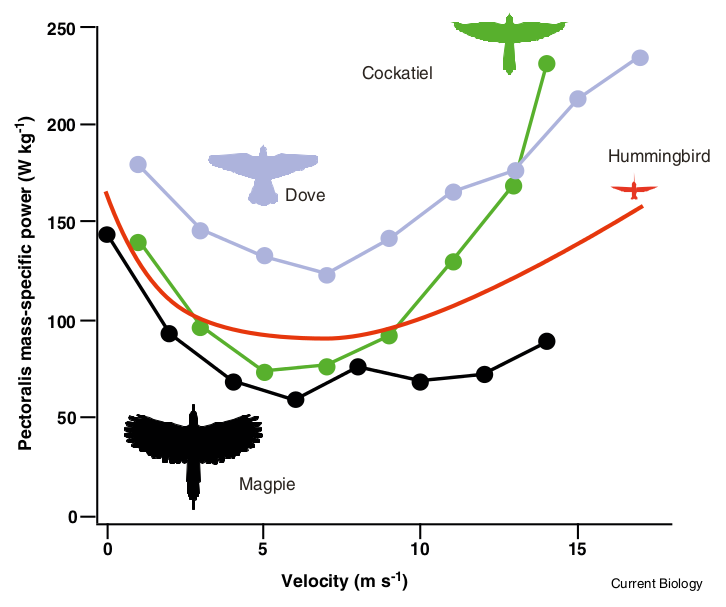
Here’s a plot of experimental data of the power consumption of different birds, as their flight speed varies.
You can see that it matches the qualitative predictions of the toy model.
But we can do more than this, and actually extract quantitative predictions from the model. An undergraduate schooled in calculus should be able to work out that special optimal speed at which energy consumption is a minimum. David MacKay plugs in the numbers in his book, and finds that the optimal speed of an albatross is about 32 mph, and for a Boeing 747 is about 540 mph. Both these numbers are remarkably close to the real values. Albatrosses fly at about 30-55 mph, and the cruise speed of a Boeing 747 is about 567 mph.
That’s a lot of mileage from a toy model!
And with this physicsy interlude into the world of albatrosses, hummingbirds, and jet planes, we come back to the question of the fuel efficiency of Boeing’s new aircraft.
You can actually use the model to work out the fuel efficiency of a plane. What you find is that it really just depends on a few factors: the shape and surface of the plane, and the efficiency of its engine. And of these factors, the engine efficiency plays the biggest role. So we would predict that engine efficiency, followed by improvements in body design might drive Boeing’s fuel savings.
This agrees with Boeing’s own assessment.
New engines from General Electric and Rolls-Royce are used on the 787. Advances in engine technology are the biggest contributor to overall fuel efficiency improvements.
New technologies and processes have been developed to help Boeing and its supplier partners achieve the efficiency gains. For example, manufacturing a one-piece fuselage section has eliminated 1,500 aluminum sheets and 40,000 – 50,000 fasteners.
Try as we like, we can’t squeeze a lot of improvement out of airplanes. Engines are already remarkably efficient, and you certainly can’t shrink the size of a plane by much, as economy class passengers can well attest. New manufacturing techniques could cut the amount of drag on the plane’s surface, but these improvements would only raise fuel efficiency by about 10%.
To quote David Mackay,
The only way to make a plane consume fuel more efficiently is to put it on the ground and stop it. Planes have been fantastically optimized, and there is no prospect of significant improvements in plane efficiency.
A 10% improvement? Yes, possible. A doubling of efficiency? I’d eat my complimentary socks.
References
I based this blog post on material I learnt from David MacKay’s fantastically clear book, Sustainable Energy without the Hot Air. It’s available online for free, and is highly recommended for anybody looking to use numbers to understand energy.
David MacKay (2009). Sustainable Energy – Without the Hot Air UIT Cambridge Ltd
I used this tip to make those XKCD style plots.
